Lernziele

Flächenproblem

• Sie wissen, was unter einem Intervall verstanden wird, und können Intervalle in der Intervallschreibweise [𝑎, 𝑏] und der Mengenschreibweise {𝑥 ∈ ℝ | 𝑎 ≤ 𝑥 ≤ 𝑏} darstellen.
• Sie deuten die Gesamtänderung einer Grösse als Flächeninhalt zwischen dem Graphen der lokalen Änderungsrate dieser Grösse und der 𝑥-Achse (Beispiel: zurückgelegte Strecke in einem Geschwindigkeits-Zeit-Diagramm).

Riemann-Integral

• Sie kennen die Begriffe Untersumme und Obersumme und können sie mit einer Skizze erklären.
• Sie wissen, dass man unter dem Integral der Funktion 𝑓 zwischen den Grenzen 𝑎 und 𝑏 den gemeinsamen Grenzwert von Unter- und Obersumme versteht.
• Sie kennen die Integralschreibweise

und wissen, was mit den Bezeichnungen Integrand, Integrationsvariable und (untere und obere) Integrationsgrenze gemeint ist.

Wichtige Begriffe

• Sie kennen die Begriffe Stammfunktion, Integrationskonstante, bestimmtes und unbestimmtes Integral.
• Sie wissen, was der Hauptsatz der Differenzial- und Integralrechnung aussagt.

Integralberechnung

• Sie wissen, wie der Flächeninhalt zwischen dem Graphen einer Funktion 𝑓 und der 𝑥-Achse für die Bestimmung eines bestimmten Integrals gezählt wird:
  • positiv für Flächen, die oberhalb der 𝑥-Achse liegen
  • negativ für Flächen, die unterhalb der 𝑥-Achse liegen
• Sie wenden die Faktor-, Summen-, Vertauschungsregel und die Intervalladditivität zur Berechnung von Integralen an.
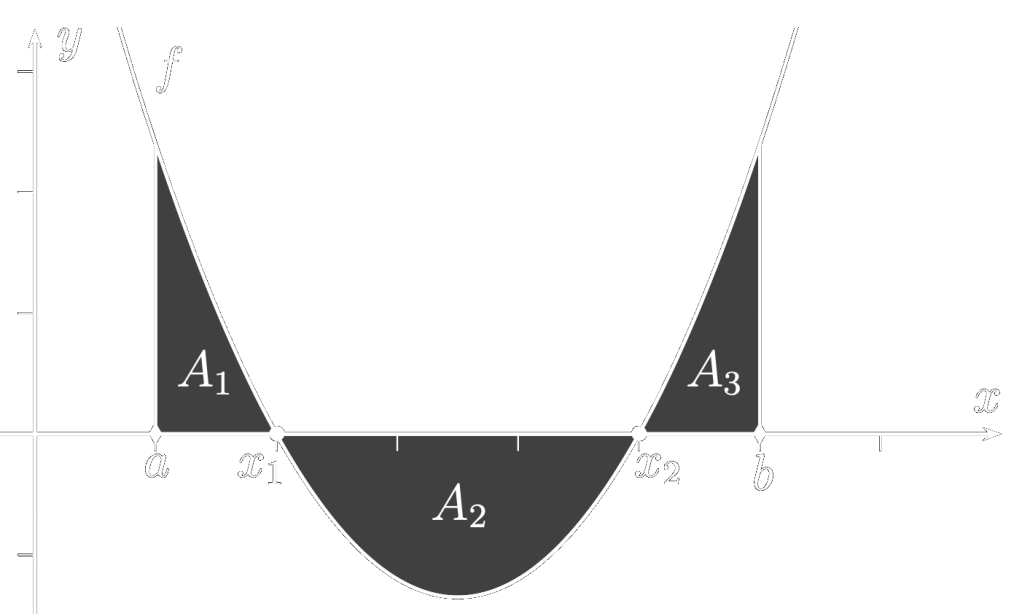
• Sie können den Flächeninhalt zwischen einem Graph und der 𝑥-Achse bestimmen, indem Sie das betrachtete Intervall an den Nullstellen unterteilen und Flächen oberhalb und unterhalb der 𝑥-Achse separat berechnen und alle positiv zählen.

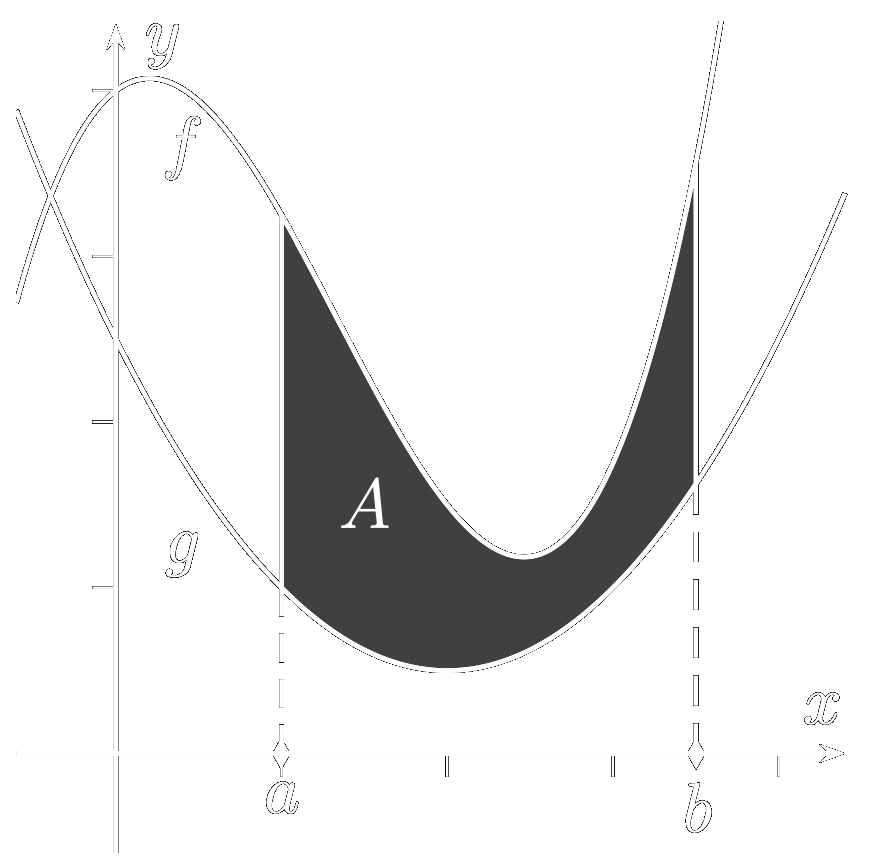
• Sie können die Fläche zwischen zwei Graphen berechnen. Gegebenenfalls berechnen Sie die Schnittpunkte der Graphen und berechnen den Betrag aller Flächenteile einzeln.